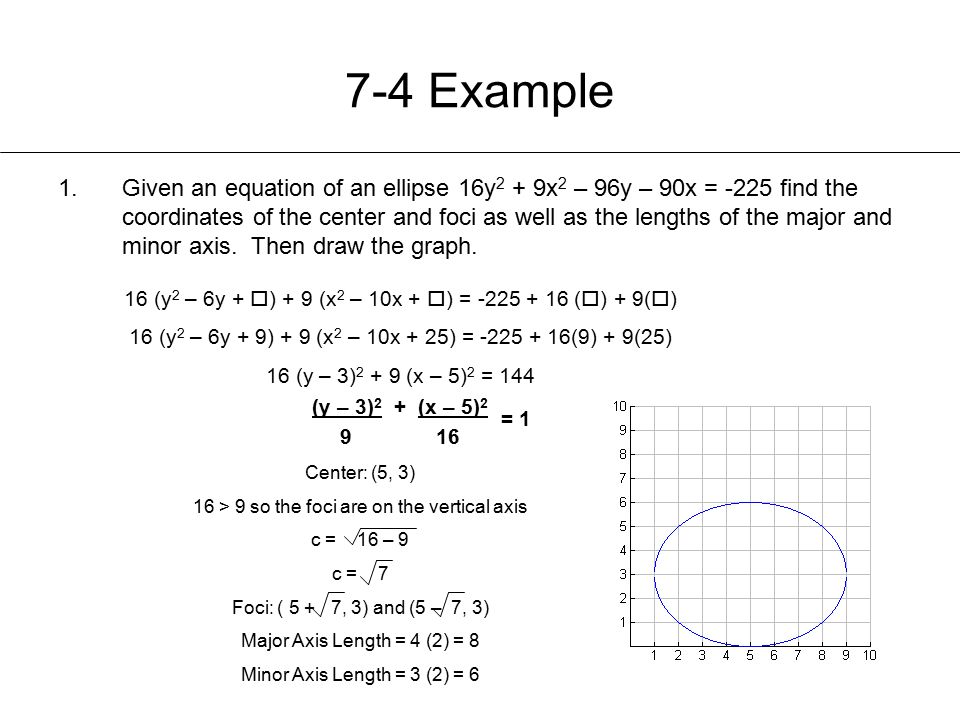
The starting system of equations is {((x3)^2(y2)^2=16),(2x2y=10) } First step is to divide the second equation by 2 to get only x and y without coefficients {((x3)^2(y2)^2=16),(xy=5) } Now we can calculate one of the variables from the second equation to substitute it in the first one {((x3)^2(y2)^2=16),(y=5x) } If we substitute we get (x3)^2(**5x**2)^2=16 (x3)^2(7x)^2=16 x^26xxx^216=0 2x^2x42=0 Now we can divide both sides by 2 x^2Start your free trial In partnership with You are being redirected to Course Hero I want toSteps for Solving Linear Equation x = 2 y 5 x = 2 y − 5 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 2y5=x 2 y − 5 = x Add 5 to both sides Add 5 to both sides

State The Type Of The Quadratic Surface X 3 2 Y 5 2 Z 8 2 1 Choose From The Following Options 1 Ellipsoid 2 Hyperboloid Of One Sheet 3 Hyperboloid Of Two Sheets 4 None Of These Study Com
X^2+(x+3)(2x-y+5)=x+16
X^2+(x+3)(2x-y+5)=x+16-2x3y316x2y432xy5 Final result 2xy3 • (x 4y)2 Step by step solution Step 1 Equation at the end of step 1 (((2•(x3))•(y3))((16•(x2))•(y4)))25xy5(3*x5)^2(16)=0 Step by step solution Step 1 11 Evaluate (3x5) 2 = 9x 230x25 Step 2 Pulling out like terms 21 Pull out like factors 9x 2 30x 9 = 3 • (3x 2 10x 3) Trying to factor by splitting the middle term 22 Factoring 3x 2 10x 3 The first term is, 3x 2 its coefficient is 3



Www Stjoeschool Org Assets Imgs Uploads 8th Grade Mr Croughn And Mr Lawrence Pdf
Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreMinimize z = x 3y 2u5z 5y 2x 2 > Subject to y 2 ALALALALAL 16 16 5 0 C y 0 Minimum is at 2= y = > Next Question Get more help from Chegg Solve itSystemofequationscalculator xy=2, 2x5y=16 en Related Symbolab blog posts High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables In this blog
Calculadoras gratuitas passo a passo para álgebra, trigonometria e cálculoGraph ( (x3)^2)/16 ( (y5)^2)/9=1 (x − 3)2 16 (y 5)2 9 = 1 ( x 3) 2 16 ( y 5) 2 9 = 1 Simplify each term in the equation in order to set the right side equal to 1 1 The standard form of an ellipse or hyperbola requires the right side of the equation be 1 1X = (3 − y) (y 5) − 5, y ≥ −5 and y ≤ 3 View solution steps Steps by Finding Square Root ( x 5 ) ^ { 2 } ( y 1 ) ^ { 2 } = 16 ( x 5) 2 ( y 1) 2 = 1 6 Subtract \left (y1\right)^ {2} from both sides of the equation Subtract ( y 1) 2 from both sides of the equation
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyStep by step solution of a set of 2, 3 or 4 Linear Equations using the Substitution Method 2x3y=5;5x−2y=−16 Tiger Algebra SolverGraph ((x5)^2)/4((y3)^2)/16=1 Simplify each term in the equation in order to set the right side equal to The standard form of an ellipse or hyperbola requires the right side of the equation be This is the form of an ellipse




Grade 8 Unit 4 Practice Problems Open Up Resources




Vectors And The Geometry Of Space Monografias Com
Steps for Solving Linear Equation 2x3y = 5 2 x 3 y = 5 Subtract 3y from both sides Subtract 3 y from both sides 2x=53y 2 x = 5 − 3 y Divide both sides by 2 Divide both sides by 2Move all terms containing x to the left, all other terms to the right Add 'y' to each side of the equation 3x 1y y = 16 y Combine like terms 1y y = 0 3x 0 = 16 y 3x = 16 y Divide each side by '3' x = y Simplifying x = yAlgebra Write the Equation in Standard Form y= (x5)^216 y = (x − 5)2 16 y = ( x 5) 2 16 To write an equation in standard form, move each term to the right side of the equation and simplify y = ax2 bxc y = a x 2 b x c Simplify (x −5)2 16 ( x 5) 2 16




य द X 3 2 Y 5 2 Z 4 2 0 ह त X 2 9 Y 2




Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1
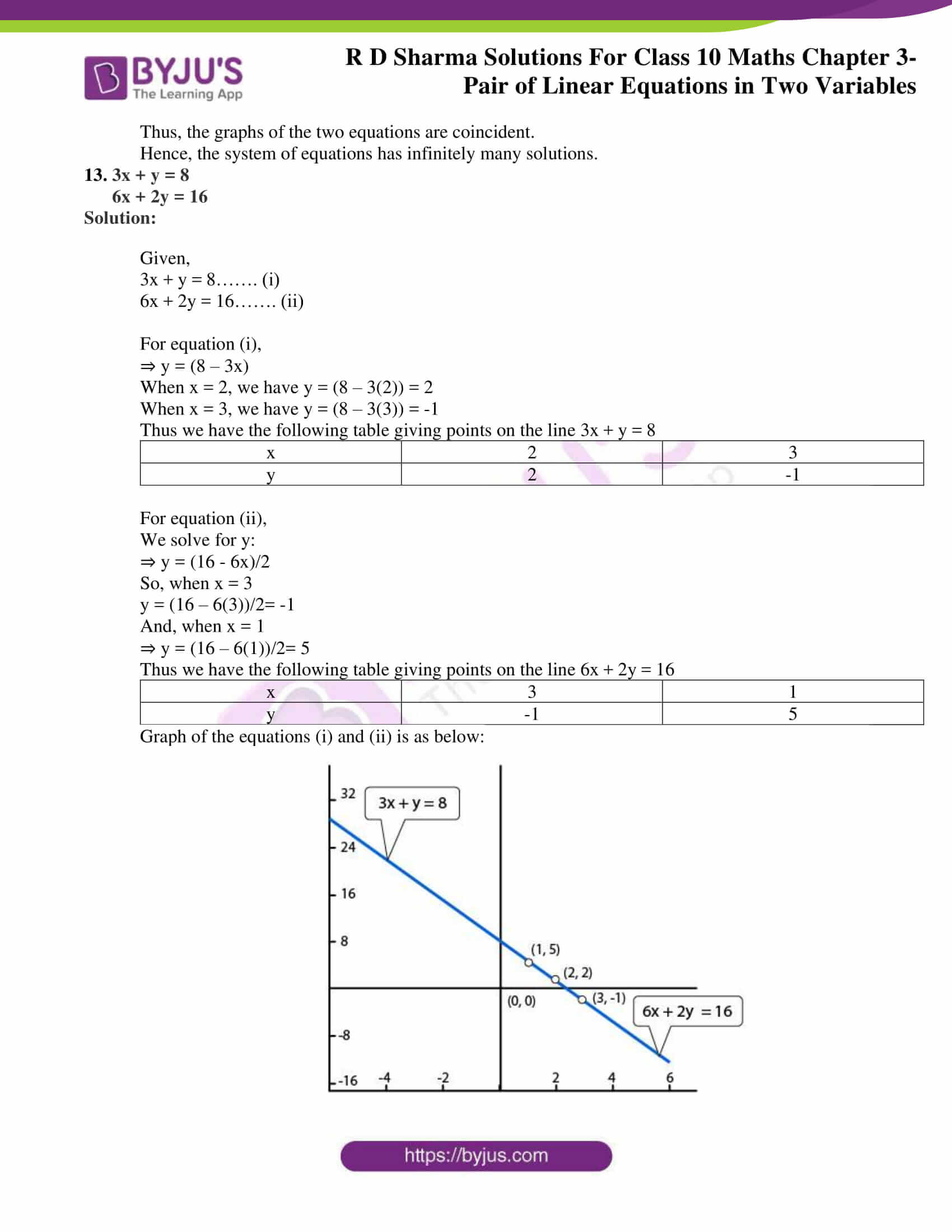
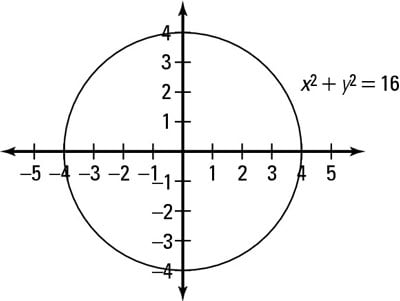
2(5) 3y = 16 10 3y = 16 3y = 6 y = 2 So our solution is (5,2) or ELIMINATION METHOD xy =3 2x3y=16 I'm going to eliminate the y Multiply the top equation by 3 3(xy = 3) 2x3y = 16Simplify 3x3y=9 2x3y=16 Add the two equations together 5x 0y = 25 x = 5 Then substitute x=5 back into one of the original equations, let's use theOur online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!In the twodimensional coordinate plane, the equation x 2 y 2 = 9 x 2 y 2 = 9 describes a circle centered at the origin with radius 3 3 In threedimensional space, this same equation represents a surface Imagine copies of a circle stacked on top of each other centered on the zaxis (Figure 275), forming a hollow tube




Answered Find The Equations Of Planes That Just Bartleby




The Graph Of The Equation X 2 16 Y 2 9 1 Chegg Com
Start your free trial In partnership with You are being redirected to Course Hero I want to submit the same problem to Course Hero CancelSolution for y2=35(x5) equation Simplifying y 2 = 35(x 5) Reorder the terms 2 y = 35(x 5) Reorder the terms 2 y = 35(5 x) 2 y = (5 * 35 x * 35) 2 y = (175 35x) Solving 2 y = 175 35x Solving for variable 'y' Move all terms containing y to the left, all other terms to the rightMaximize 5 3x 4y x^2 x y y^2 WolframAlpha Have a question about using WolframAlpha?




Evaluate The Volume Of The Solid Bounded By Z 8 X 2 Y 2 Z X 2 Y 2 X 1 Y Sqrt 3 X Y 0 Mathematics Stack Exchange



Www Lcps Org Cms Lib4 Va Centricity Domain 3279 Notes 10 7key Pdf
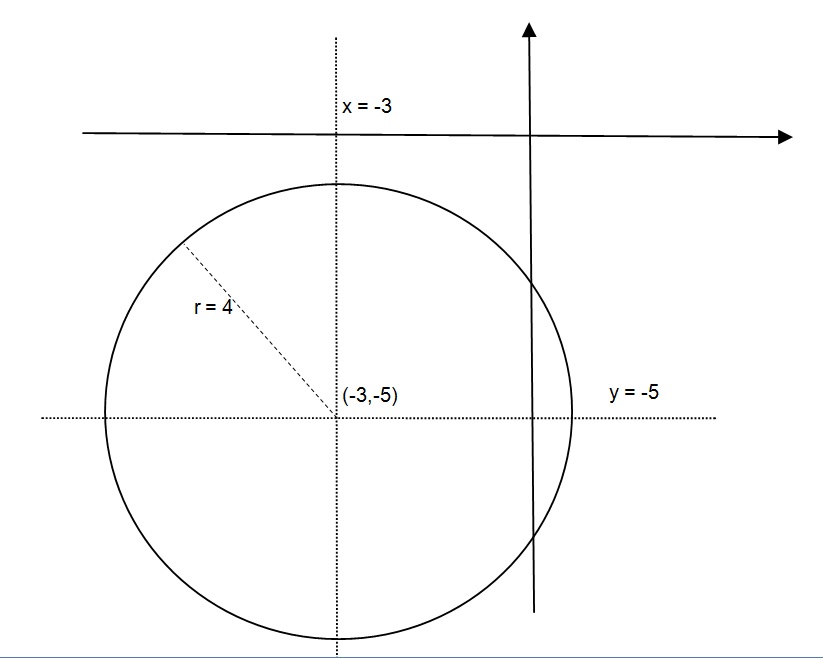
The centre of the ellipse #(xh)^2/a^2(yk)^2/b^2=1# is #(h,k)# The two axes are #2a# and #2b# and major axis is the greater of the two Vertices are #(ha,k)# and #(h,kb)# Here those along major axis are called vertices and those along minor axis are called covertices #(x2)^2/16(y5)^2/=1# can be written as #(x2)^2/4^2(y5)^2The original circle is centered at (3,5) with a radius of 4 Reflecting across the y=2 shifts the y coordinate of the center The center is 3 units above the line y=2 The reflected circle will have the center 3 units below the line y=2 I leave it to you to determine the sumRearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation (x3)*2 (y5)*2 (16)=0




This Is Conic Sections Chapter 8 From The Book Advanced Algebra Index Html V 1 0 Pdf Free Download



Http Www Standrewspaisley Com Uploads 6 0 2 3 Circle Pupil Booklet Pdf
Trigonometry Graph (x3)^2 (y5)^2=16 (x − 3)2 (y − 5)2 = 16 ( x 3) 2 ( y 5) 2 = 16 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard form The variable r r represents the radius of the circle, h h represents the xoffset from the origin, and k kFirst type the equation 2x3=15 Then type the @ symbol Then type x=6 Try it now 2x3=15 @ x=6 Clickable Demo Try entering 2x3=15 @ x=6 into the text box After you enter the expression, Algebra Calculator will plug x=6 in for the equation 2x3=15 2(6)3 = 15 The calculator prints "True" to let you know that the answer is right More Examples a) compared to the graph of f=1/x the grapg of y=3/x4 is vertical stretch by factor of 3 and a translation of 4 units left b) compared to the graph of y=1/x the graph of 3/x4 is a math The graph of y=x^2 is transformed by a stretch of scale factor 2 parallel to the x axis, followed by a translation of (0 3)



Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf




Cc1 3 Parent Guide Full Pages 101 150 Flip Pdf Download Fliphtml5
Polynomial Roots Calculator 23 Find roots (zeroes) of F (x) = x32x216x16 Polynomial Roots Calculator is a set of methods aimed at finding values of x for which F (x)=0 Rational Roots Test is one of the above mentioned tools It would only find Rational Roots that is numbers x which can be expressed as the quotient of two integers11 The equation of a circle is (x 3)2 y2 8 The coordinates of its center and the length of its radius are 12 The equation of a circle is (x 2)2 (y 5)2 32 What are the coordinates of the center of this circle and the length of its radius?Y=3 (x5) (x2) Simple and best practice solution for y=3 (x5) (x2) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it



Practice Mathnmind



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2
2^x 3^y = 5 2^x2 3^y1 = 18 Which can be written as 2^x2^2 3^y3^1 = 18 42^x 33^y = 18 Now, let's assume 2^x =m 3^y=n So, when we replace the above, we get two equations mn=5 4m3n=18 On solving the simultaneous equations, we get m=3 n=2 Now, 2^x = 3 x = log 3 to the base 2 x = log 3/log 2 x= 158 3^y=2 y = log 2 to the base 3 Explanation This equation can be recognised as the standard equation for a circle, which is (x −h)2 (y −k)2 = r2, where (h,k) is the centre of the circle and r is the radius The example is therefore a circle with centre ( −3, − 5) and radius 4 Answer linkCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history




Circles Pi Circle Words Rounding Refresher Area Perimeter



Quadratic Function
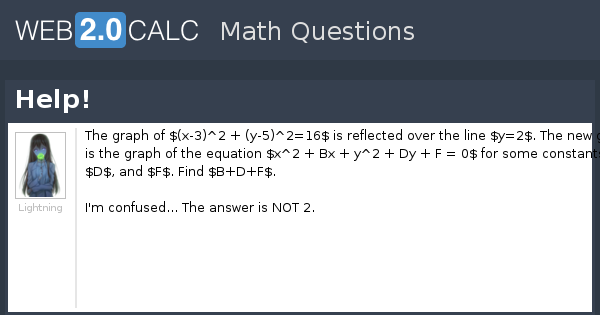
16 Suppose the relationship between variables Y, X, Xz and U is given by the following model Y = 52 (X2)2 3 X2 U U Uniform(1 X X2,1 X X2) X1 Uniform(0,2) X, Uniform(04) Answer the following questions (explaining your answers), or do what is asked 1 Transcript Example 17 Solve the pair of equations 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 2/𝑥 3/𝑦=13 5/𝑥−4/𝑦=−2 So, our equations become 2u 3v = 13 5u – 4v = –2 Hence, our equations are 2u 3v = 13 (3) 5u – 4v = – 2 (4) From (3) 2u 3v = 13 2u = 13 – 3V u = (13 − 3𝑣)/2SOLUTION The graph of (x3)^2 (y5)^2=16 is reflected over the line y=2 The new graph is the graph of the equation x^2 Bx y^2 Dy F = 0 for some constants B, D, and F Find BDF



Solve The Following System Of Linear Equations In Three Variables I X Y Z 5 2x Y Z 9 X 2y 3z 16 Sarthaks Econnect Largest Online Education Community




Graph Y X 2 2 16 Please Help Brainly Com
Graph (x3)^2 (y1)^2=16 (x − 3)2 (y − 1)2 = 16 ( x 3) 2 ( y 1) 2 = 16 This is the form of a circle Use this form to determine the center and radius of the circle (x−h)2 (y−k)2 = r2 ( x h) 2 ( y k) 2 = r 2 Match the values in this circle to those of the standard formNow, applying the Square Root Principle to Eq #321 we get x5 = √ 16 Subtract 5 from both sides to obtain x = 5 √ 16 Since a square root has two values, one positive and the other negative x 2 10x 9 = 0 has two solutions x = 5 √ 16 or x = 5 √ 16 Solve Quadratic Equation using the Quadratic Formula 33 Solving x 2Circleequationcalculator center (x2)^2(y3)^2=16 en Related Symbolab blog posts My Notebook, the Symbolab way Math notebooks have been around for hundreds of years You write down problems, solutions and notes to go back



Ellipses




Vectors And The Geometry Of Space Monografias Com
X^3 x^2 y x y^2 y^3 Extended Keyboard;13 Circle O is represented by the equation (x 3)2 (y 5)2 48 The coordinates of the (x a)^2 (y b)^2 = r^2 where (a,b) = the point where the center of the circle lies r = radius From the equation, (x 3)^2 (y 5)^2 = 16 r^2 = 16 r = 4 units Recall that the circumference of a circle is given by C = 2*pi*r Substituting, C = 2*314*2 C




Test Mu Alpha Theta




2 1 R 2 16 R 0 0 R 2 25 R Special Pythagorean Triple Ppt Download
Move all terms containing x to the left, all other terms to the right Add '15' to each side of the equation 15 15 6x = 16 15 Combine like terms 15 15 = 0 0 6x = 16 15 6x = 16 15 Combine like terms 16 15 = 31 6x = 31 Divide each side by '6' x = Simplifying xSimple and best practice solution for 3(3x2)=165x equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, soGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!




Show Tha X 5 Y 2 Is A Solution Of The System Of Line




Answered 3 1 X 6 2 Y 5 2 16 In The Xy Plane Bartleby
1) The graph of (x3)^2 (y5)^2=16 is reflected over the line y=2 The new graph is the graph of the equation x^2 Bx y^2 Dy F = 0 for some constants B, D, and F Find BDF 2) Geometrically speaking, a parabola is defined as the set of points that are the same distance from a given point and a given lineCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music2 3\pi e x^{\square} 0 \bold{=} Go Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!
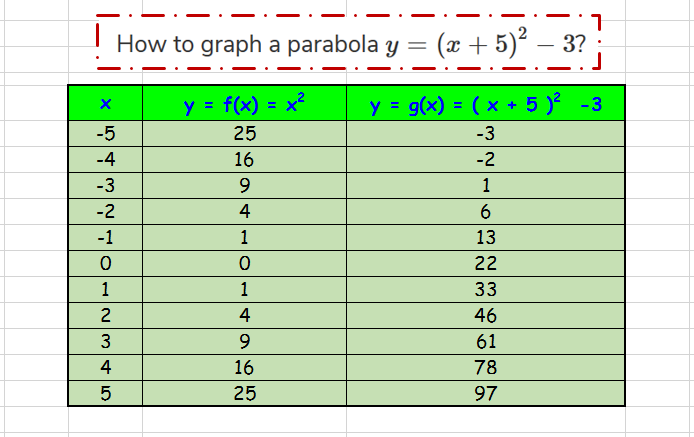



How To Graph A Parabola Y X 5 2 3 Socratic




Solve Each System By The Method Of Your Choice Chegg Com
2 x 3 2 y k 2 r 2 x h 2 16 9 r2 25 r2 5 ry 5 2 5 2 x 3 2 y 5 2 25 x 3 2 General from MATH SECTION 1 at Anderson High School, CincinnatiThe circle (x 3)^2 (y 5)^2 = 16 can be drawn with parametric equations Assume the circle is traced clockwise as the parameter increases If x = 3 4 cos t then y = Get more help from Chegg Solve it with our calculus problem solver and calculator To convert from Cartesian to Polar coordinates use the following formulae that link them ∙ x = rcosθ and y = rsinθ x2 y2 − 8y 16 = 16 (expanding bracket) ⇒ r2cos2θ r2sin2θ − 8rsinθ 16 −16 = 0 then r2(cos2θ sin2θ) − 8rsinθ = 0 using the identity cos2θ sin2θ = 1 ⇒ r2 = 8rsinθ and dividing both sides by r



Www Stjoeschool Org Assets Imgs Uploads 8th Grade Mr Croughn And Mr Lawrence Pdf




Q227 If X 3 2 Y 5 2 Z 4 2 0 Then The Value Of X2 9 Y2 25 Z2 16 Algebra Gravity Coaching Youtube




What Is The Equation Of A Circle With Center 3 5 And Radius 4 Brainly Com



Solved X 6 2 Y 5 2 16 In The X Y Plane




Geometry 10 6 Equations Of A Circle Ppt Download



2



Www Gpschools Org Cms Lib Mi Centricity Domain 664 11 7 worksheet key Pdf




State The Type Of The Quadratic Surface X 3 2 Y 5 2 Z 8 2 1 Choose From The Following Options 1 Ellipsoid 2 Hyperboloid Of One Sheet 3 Hyperboloid Of Two Sheets 4 None Of These Study Com



2 Ways To Graph A Circle Dummies




Solve Initial Value Problem Ivp Dy 2y H Dx V X2 16 0 Y 5 Homeworklib



How Do You Graph X 3 2 Y 5 2 16 Example
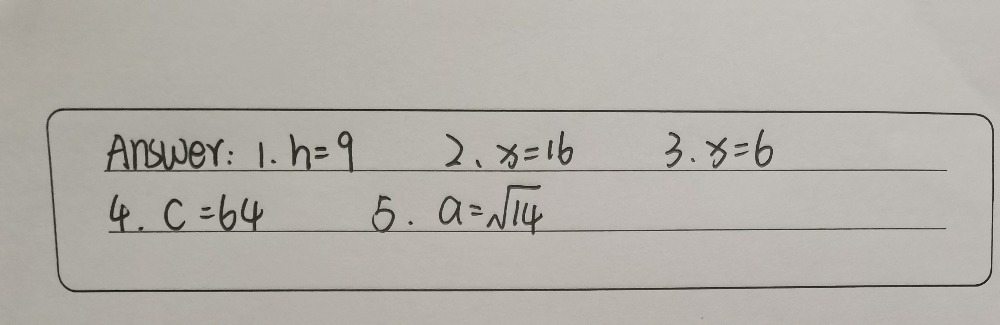



Directior S R Efer To The Diaaram Then Find The I Gauthmath




2 Using A 2r Y Z 4 3x 2y 32 16 1 X 3y 2z 12 Iii 2r 3y Z 9 4r Y 7 X 3y 72
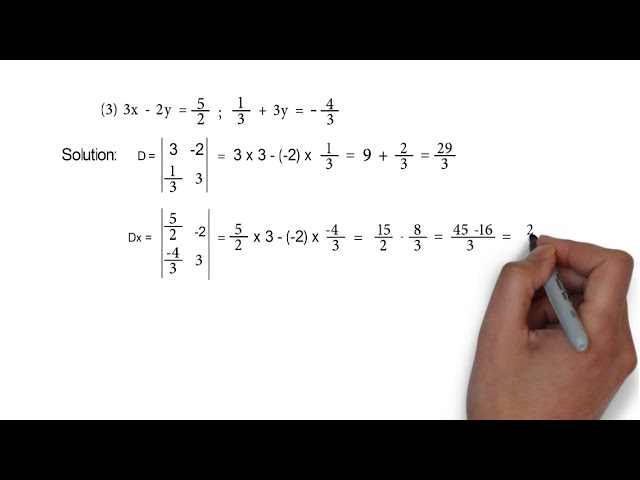



3x 2y 5 2 And 1 3 3y 4 3 Problem Set 1 Q5 3 Linear Equation In Two Variables Youtube



Http Www Nicolet K12 Wi Us Faculty Dgibbon Circle ellipse answer sheet pdf Pdf




Hyperbolas




Find The Center Vertices And Foci Of The Ellipse Chegg Com



Www Deerfield K12 Wi Us Faculty Polzinr Cms Files Assignment Attach 330 Final review key Pdf
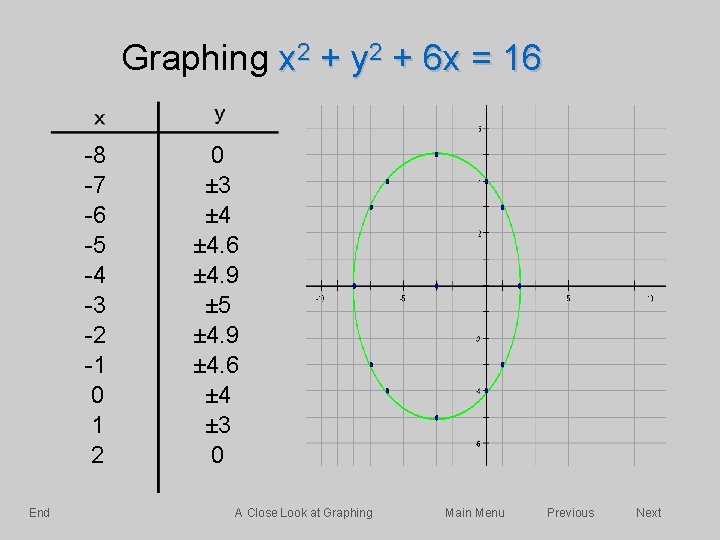



Skip Introduction A Closer Look At Graphing The
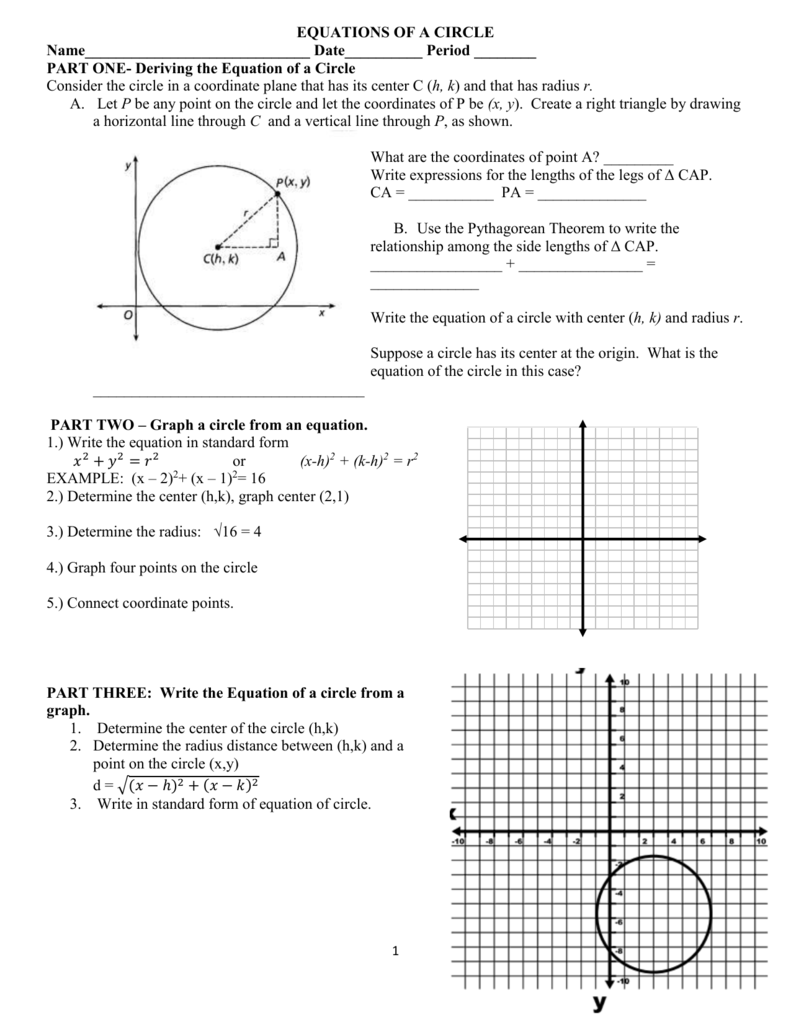



X 3 2 Y 1




Graphing Parabolas



Solution Please Im Asking For Your Guys Devine Help Your Assisstance Would Be Very Very Important To Me So Please Offer Me A Helping Hand 1 Find The Foci Of An Ellipse With The Equation



2
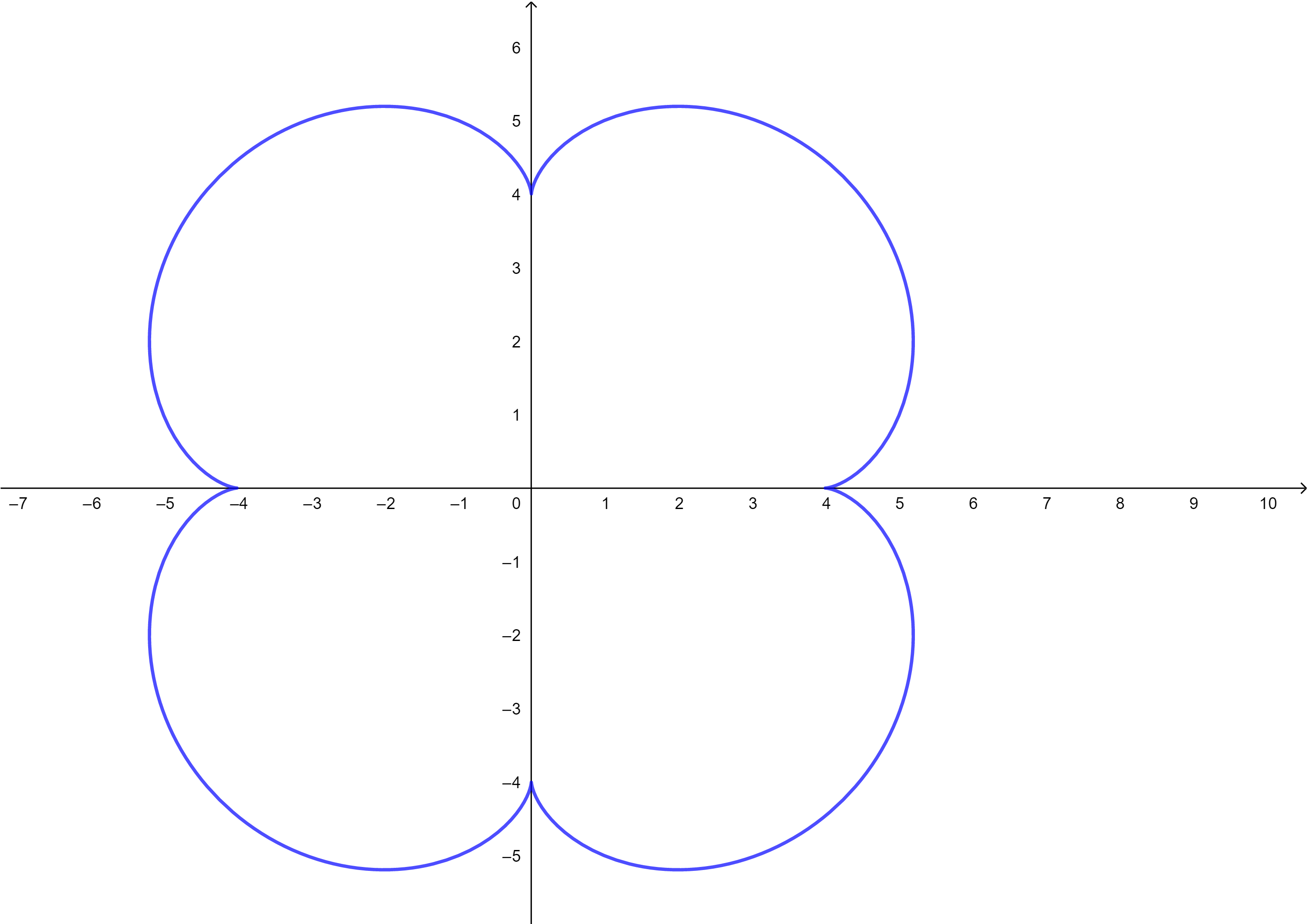



If A Circle C With Radius 1 Rolls Along The Outside Of The Circle X 2 Y 2 16 A Fixed Point P On C Traces Out A Curve Called An Epicycloid With Parametric Equations X




Solutions For Appendix Implicit




Geometry Mini Lesson Circle C Is Defined By The Equation X 4 2 2 Y 5 1 2 36 Which Of The Following Identifies The Center C H K And Radius Ppt Download
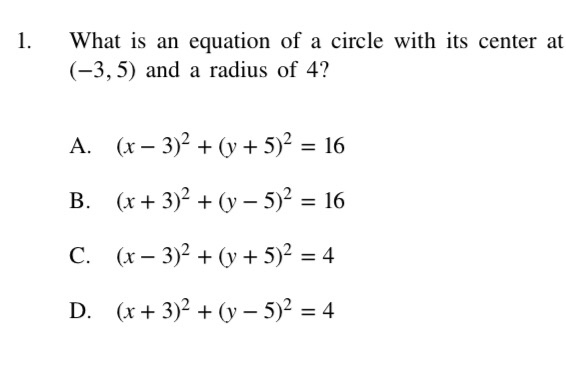



1 What Is An Equation Of A Circle With Its Center At Chegg Com



Http Www Everettsd Org Cms Lib07 Wa Centricity Domain 959 Circles review worksheet Pdf



Http Www Cusd80 Com Cms Lib6 Az Centricity Domain 2148 Q1 exam review 13 14 key pdf Pdf




Determine Whether The Statement Is True Or False The Circle X 2 2 Y 3 2 16 Intersects The Brainly Com




View Question 1 The Graph Of X 3 2 Y 5 2 16 Is Reflected Over The Line Y 2 The New Graph Is The Graph Of The Equation X 2 Bx Y 2 Dy F 0 For Some Constants
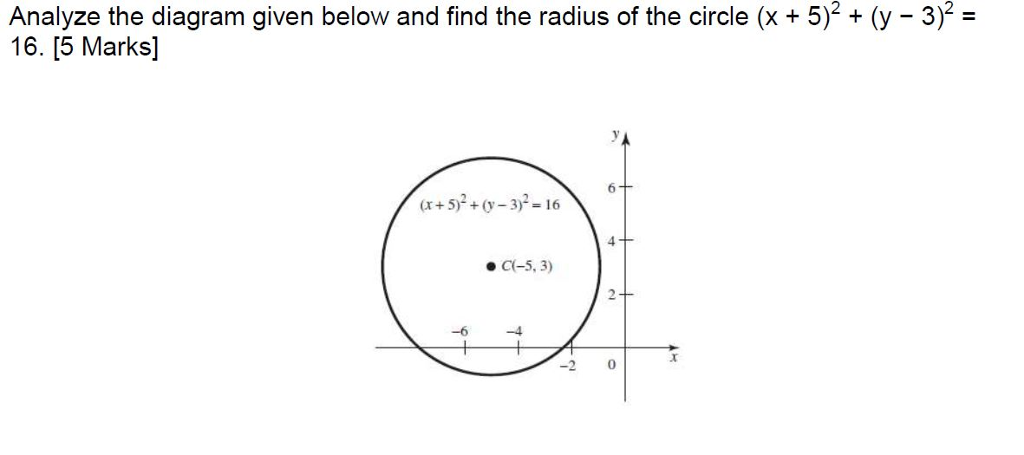



Analyze The Diagram Given Below And Find The Radius Chegg Com




Askhseis Sthn Paragontopoihsh




Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1
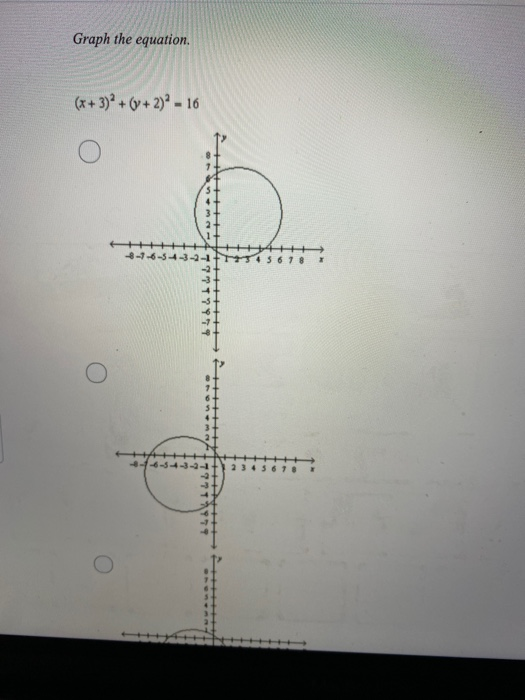



Graph The Equation X 3 2 Y 2 16 Chegg Com



Solution Graph The Relation Defined By The Equation X 2 Y 3 2 16 Express The Domain And The Range Of This Relation In Set Builder Notation



Www Brewtoncityschools Org Cms Lib Al Centricity Domain 133 10 8 Equations Of Circle Pdf




Solutions Manual For Calculus For Business Economics And The Social A




Solutions Manual For Calculus For Business Economics And The Social A




1 Equation Of A Circle Flashcards Quizlet
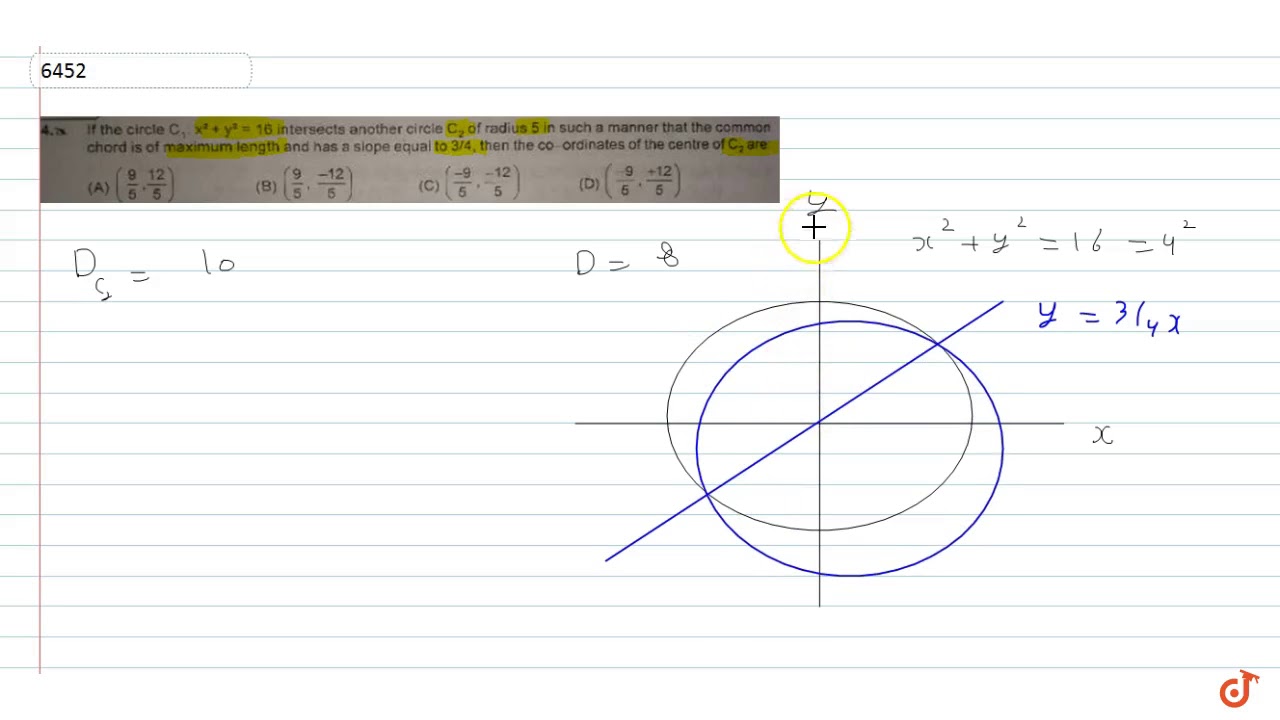



If The Circle C1 X 2 Y 2 16 Intersect Another Circle C2 Of Radius 5 In Such A Way That Comm Youtube



Http Www Unit5 Org Cms Lib03 Il Centricity Domain 2651 Semester 1 review 15 solutions Pdf



2



What Will Be The Equation Of A Circle Concentric With The Circle Math X 2 Y 2 4x 6y 9 0 Math And Passing Through The Point Math 4 5 Math Quora



Http Www Exeter K12 Pa Us Cms Lib6 Pa Centricity Domain 604 Wks section 5 5 5 6 review Pdf



Www Jmap Org Worksheets A Rei C 7 Quadratic Linearsystems5a Pdf



Www Deerfield K12 Wi Us Faculty Polzinr Cms Files Assignment Attach 330 Final review key Pdf
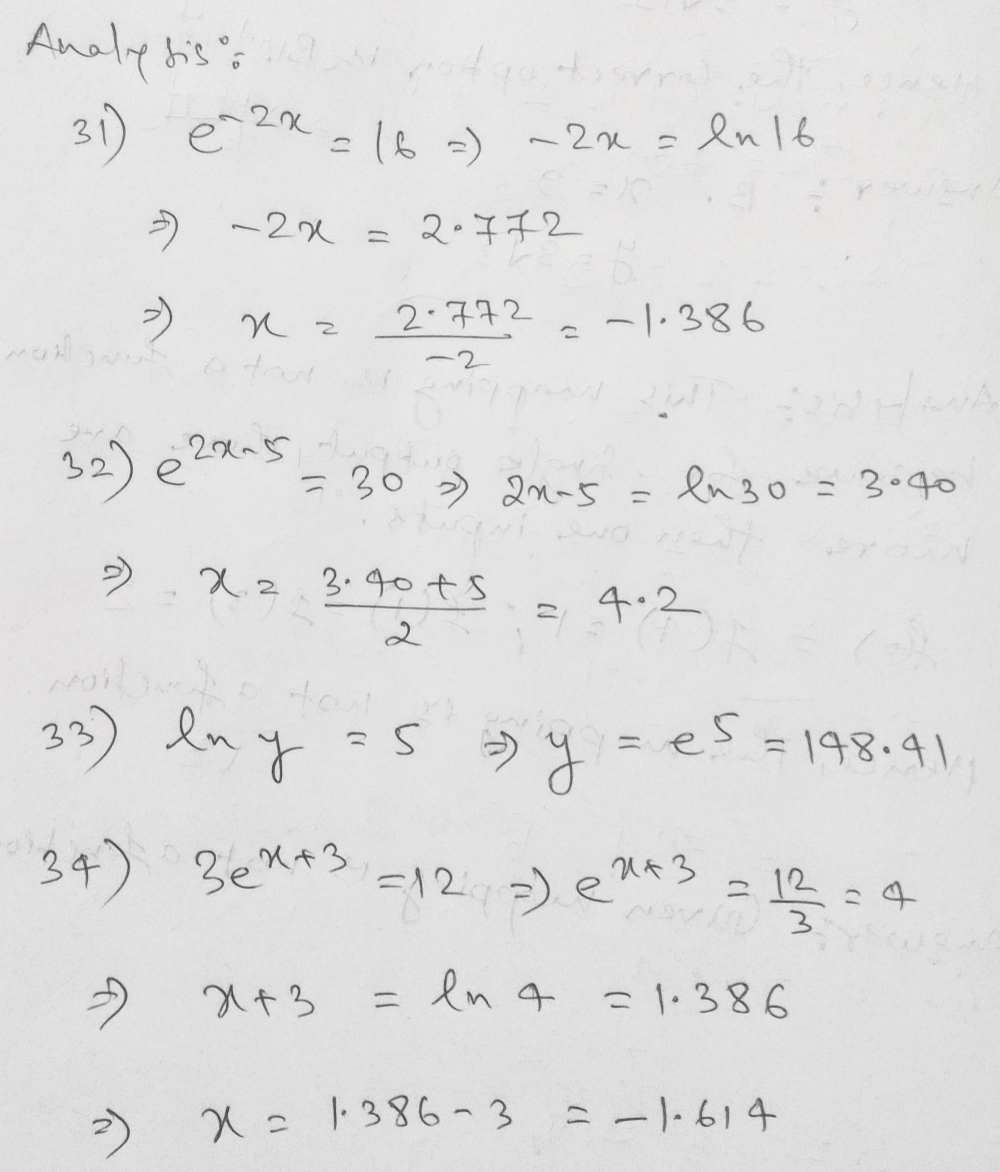



31 E 2x 16 32 E2 X 5 30 33 In Y 5 34 3ex 3 12 Gauthmath



10 Points To The Person Who Can Help Me With 4 Precalculus Questions Please Mathskey Com



Solved Example 4 5 And 6 3 Write An Equation For A Circle If The Endpoints Of A Diameter Are At Use The Midpoint Formula To Find The Cente Course Hero



Www Greeleyschools Org Cms Lib Co Centricity Domain 6012 Mod 5 lesson 17 and 18 with notes Pdf



Conics 5 Parabolas Solutions Timthemathman Com Flip Ebook Pages 1 17 Anyflip Anyflip



Http Skylinesecmath2h Weebly Com Uploads 4 1 8 8 3 12 Answers Pdf




Problems With Answers On Basic Mathematics Final Exam Math 104 Docsity



Http Www Standrewspaisley Com Uploads 6 0 2 3 Circle Pupil Booklet Pdf



How To Graph A Parabola Y 1 2 X 3 2 5 Socratic
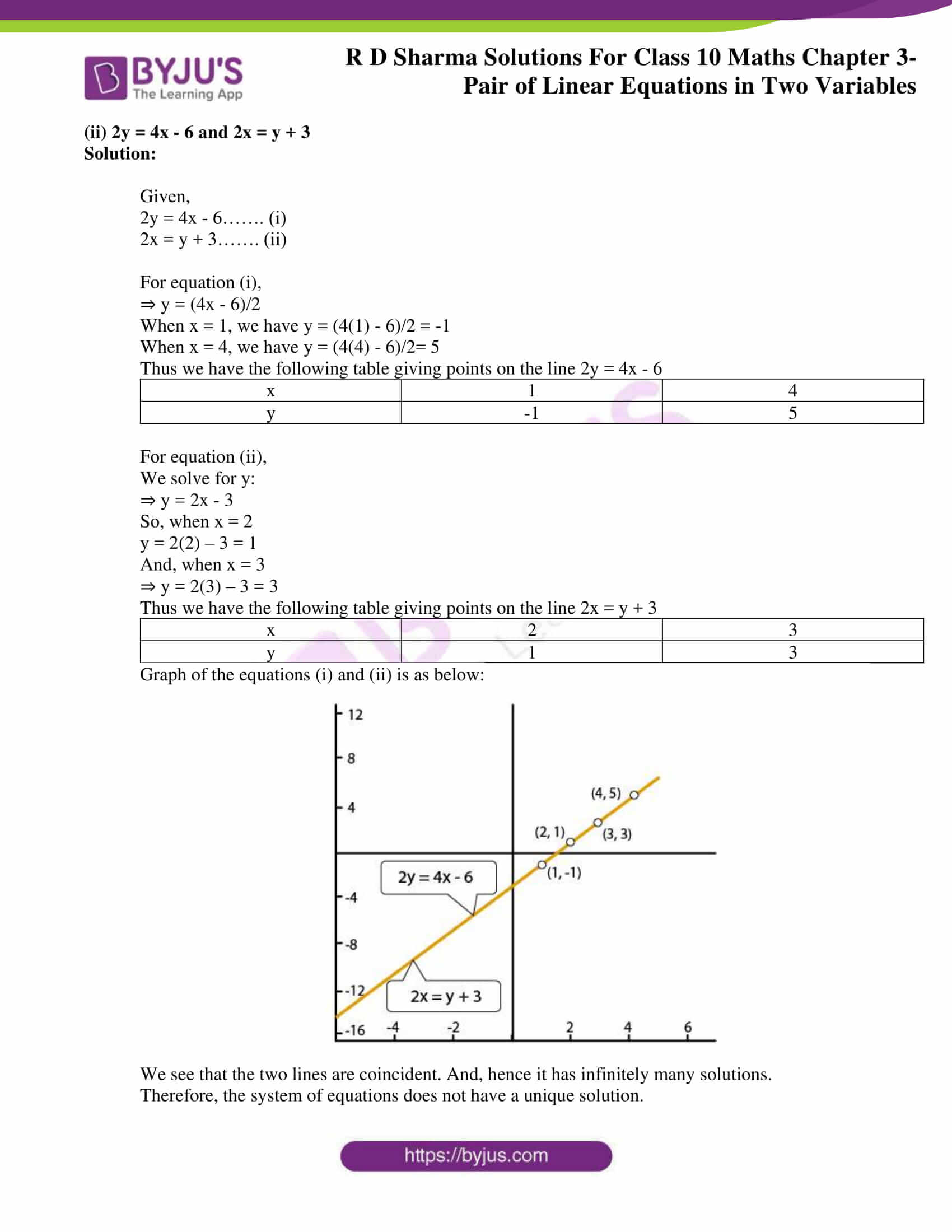



Rd Sharma Class 10 Solutions Maths Chapter 3 Pair Of Linear Equations In Two Variables Exercise 3 2




Geometry Regents Review Pdf Free Download



Http Www Eastauroraschools Org Cms Lib Ny Centricity Domain 323 Midterm 2 answers Pdf



Http Mrsaiellomath Weebly Com Uploads 3 1 4 2 86 Standard Form Of A Circle Pdf
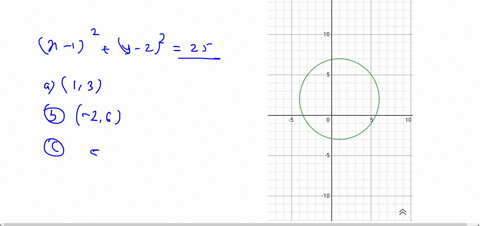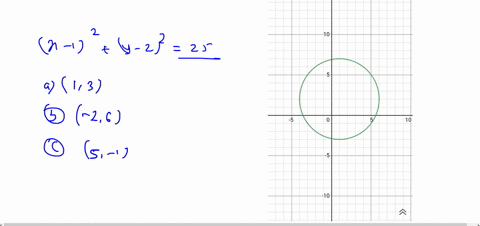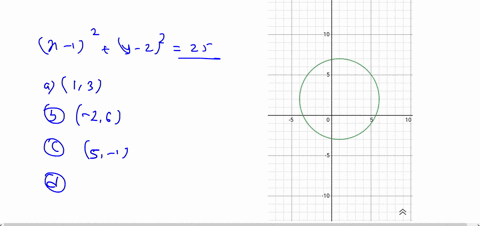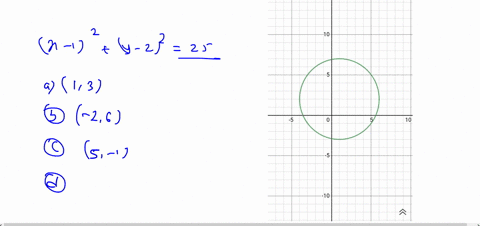



Solved X 6 2 Y 5 2 16 In The X Y Plane



Www Jessamine K12 Ky Us Userfiles 1726 Classes 11 9 lesson 24 circles Pdf Id



Http Lhsblogs Typepad Com Files Day 4 Hw Conicsworksheet1circles Pdf




Equation Of Circle Worksheet Circle Space



Chapter 7 Analyzing Conic Sections Ppt Video Online Download




College Algebra In Context 5th Edition Harshbarger Solutions Manual



Http Pollard Needham K12 Ma Us Userfiles Servers Server File Academics Math 8 accelerated review key Pdf



View Question Help
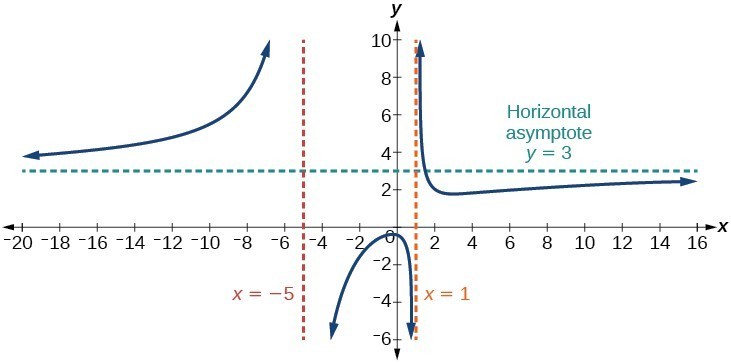



Identify Vertical And Horizontal Asymptotes College Algebra




Answered Slope Of A Line Parallel To Each Given Bartleby




Sketch The Graph Of Y X 2 2 16 Then Select The Graph That Corresponds To Your Sketch A Brainly Com



Solution Equation Of The Circle That Passes Through 9 7 And Is Tangent To Both Y Axis And The Line 3x 4y 24 0




Circle Equation Diameter Circle



What Is The Equation Of Tangents To The Circle X 2 Y 2 16 Drawn From The Point 1 4 Quora


