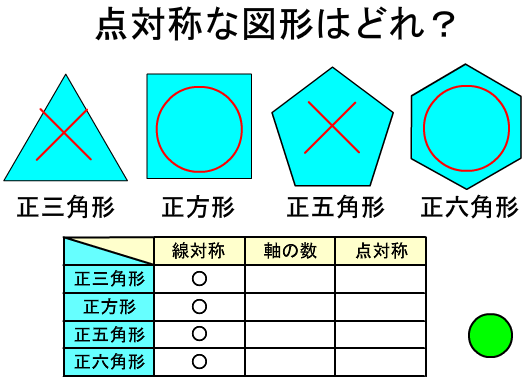
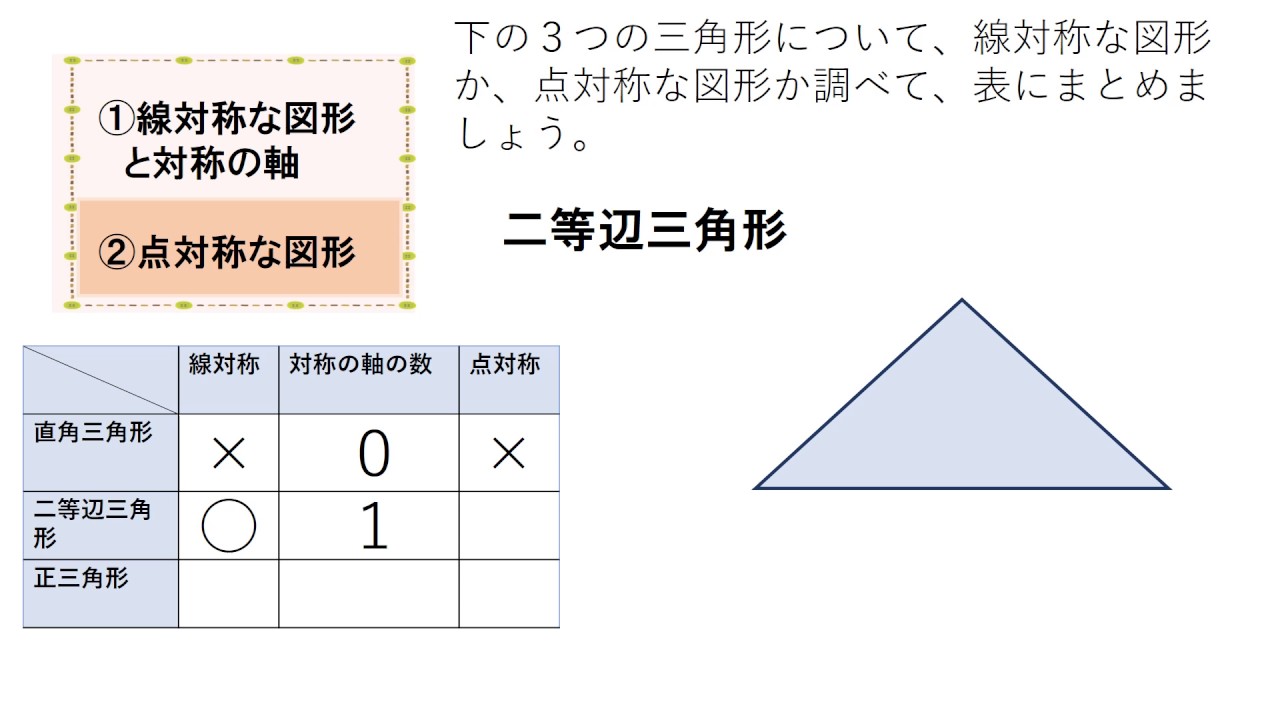
練習問題 正多角形について,線対称か点対称かを調べましょう。 線対称 軸の数 点対称 正四角形 4 正六角形 6 豊橋市算数学習プリント 算数 6年生 対称な図形⑤ 線対称 軸の数 点対称 正三角形 〇 3 × 二等辺三角形 〇 1 × 直角三角形 × ×鬼っ子チャレンジテストR2・6年・⑥ 対称な図形 名前( 解答例 ) 1 下のような四角形があります。 線対称な図形や点対称な図形には を,そうでないものには×をつけましょう。正三角形 平行四辺形 あいているらんに や ×,数を書きましょう。 いろいろな図形について,線対称な図形か点対称な図形かを調べましょう。 正五角形 正六角形 正八角形 これをもとにして 考えてみよ
Tossランド 対称な図形 多角形の性質
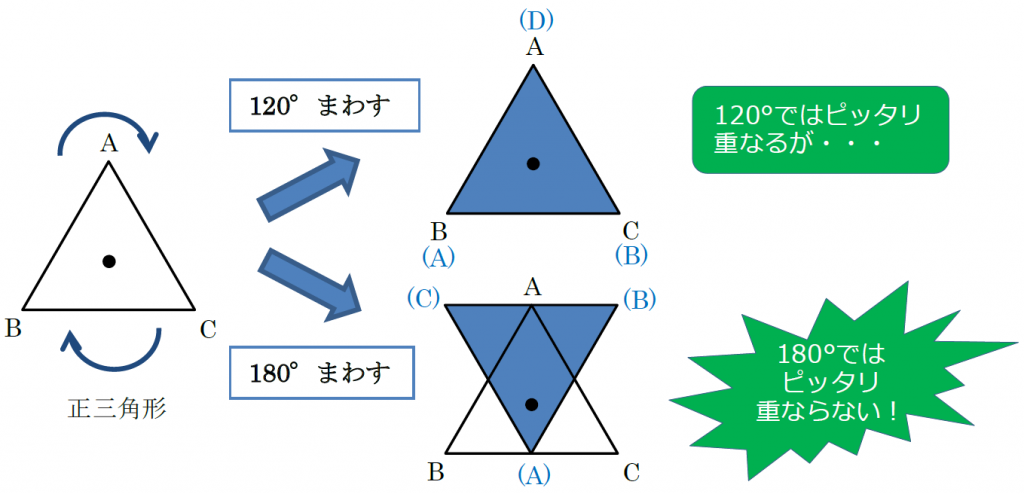
正三角形 線対称 点対称
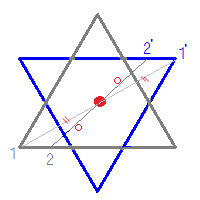
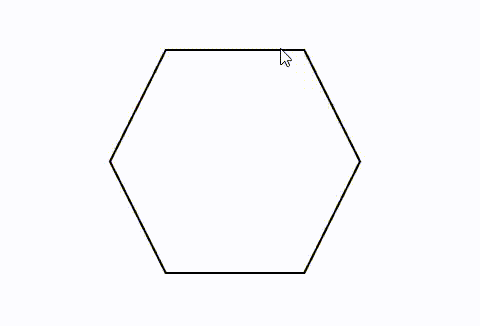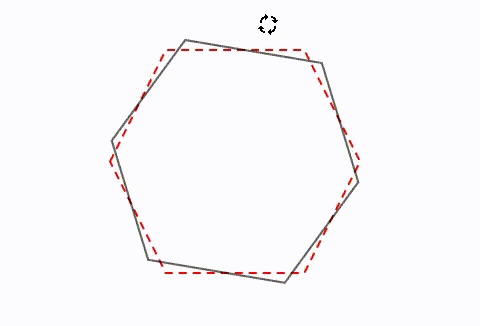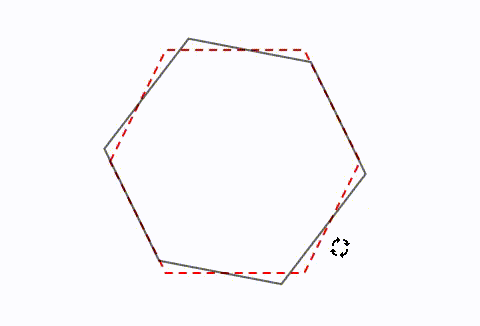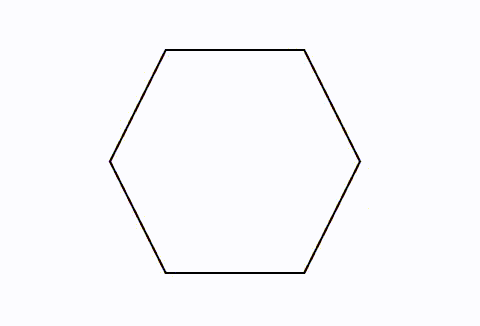
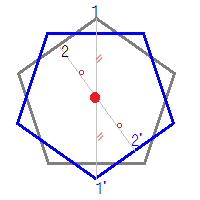
正三角形 線対称 点対称-正三角形は点対称な図形ではない. 例えば,正三角形上の点1から中心までの距離 " を中心の反対側に伸ばした点 1' は元の正三角形の上になく,点2から中心までの距離 o を中心の反対側に伸ばした点 2' も元の正三角形の上にない. このため,元の正三角形(灰色)を180°回転すると青の正三角形になり,元の図形と一致しない. だから,正三角形は点線対称 対称の軸 点対称 正方形 〇 4 〇 正六角形 〇 6 〇 正八角形 〇 8 〇 〇すべて線対称 〇対称の軸は頂点の数 〇頂点の数が偶数だったら点対称でもある。 〇頂点の数が奇数だったら点対称ではない。 自己調整の工夫



6年算数対称な図形2 正多角形教え方
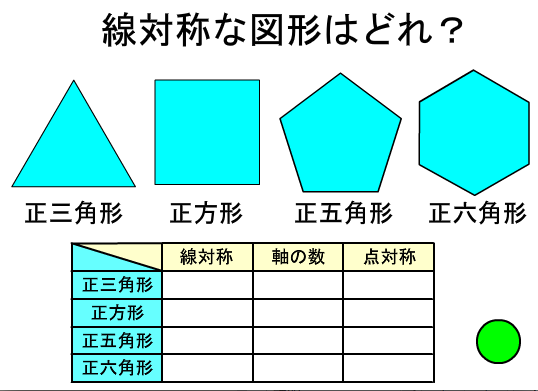
線対称かどうか 対称の軸の数本 点対称かどうか 正三角形 × × 正方形 Ø 正六角形 Ú 正八角形 Ü .正二十角形は線対称な図形です。対称の軸は何本あるでしょう? 本 ※正多角形はすべて線対称な図形。〇 1 × 正三角形 直角三角形 <問題②> 四角形が線対称か点対称か調べよう。対称な図形(10/12時) 三角形には、点対称な図形はない。 図形についても調べ 〈答え〉 ⚠ 線対称 対称の軸の数 点対称 二等辺三角形 正三角形 線対称 対称の軸の数 点対称 直角三角形 二等辺三角形 正三角形 〈気づいたこと〉 ・ ・ 〈答え〉 円は線対称、点対称な図形
円は,点対称な図形です 青⑥⑦のまとめ 線対称 対称の軸の数 点対称 ※三角形には,点対称な図形はない←これ大事‼ 😊・今日の算数は,ここまでです。よく頑張りました。 対応の軸(じく)・対象の中心 線対称 対称の 軸の数 点対称 正方形 4点Oが対称の中心になるように,点対称な図形をかきましょう。 次の図形について,下の表を完成させましょう。 正三角形 正方形 平行四辺形 ひし形 線対称かどうか × 対称の軸の本数(本) 3 4 0 2 点対称かどうか × ア算数 線対称かな? 点対称かな? の オアシス b a d c f e h g o o o 正三角形 正方形 正五角形 正六角形 正七角形 正八角形 正多角形 線対称 点対称 「線対称」でも「点対称」 でもあるのは, どんな正多角形かな? 表を見て考えてみよう!
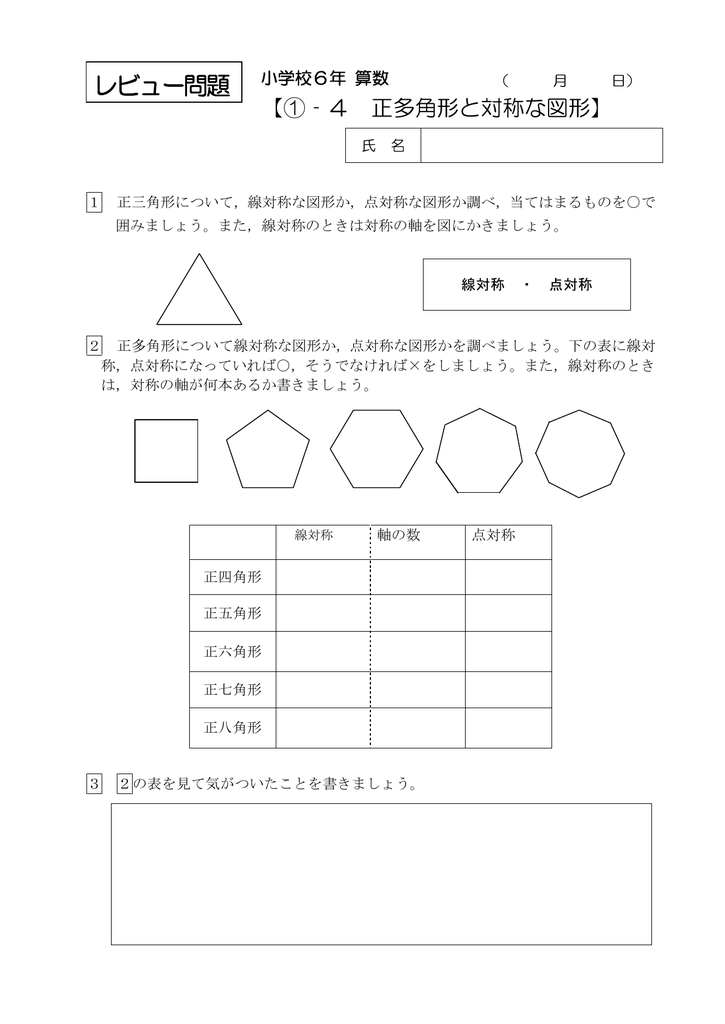
鬼っ子チャレンジテストR2・6年・① 対称な図形 名前( ) 1本の直線を折り目にして折ったとき,折り目の両側がぴったり重なる 図形は,線対称であるといいます。 また,その折り目にした直線を,対称の軸といいます。 線対称な図形では,対応する辺の長さは等しくなっています。 また,対応する角の大きさも等しくなっています。 線対称な図形では,対応P19 3 多角形と対称 問題 1 これまでに学習した多角形について t線対称な図形か点対称な図形か調べましょう u 課題 これまでに学習した図形を線対称な図形か点対称な図形かに注目して見直そう(1)点o を対称の中心とした点対称な図形の残りの半分をかきましょう。 (2)次の正多角形について,線対称や点対称のときは ,そうでないときは×をかきま しょう。また,線対称のときは,対称の軸の数をかきましょう。 線対称 対称の軸の数(本) 点対称 正四角形(正方形) 正五角形 正六角形 (例) o




6年算数 対称な図形 10時間目 正多角形や円について それぞれ線対称 点対称という見方で調べてみましょう Youtube



点対称な図形
点 対称な図形 1① ₁ 右の図は,直線アイを対 たい 称 しょう の軸 じく とした 線対称な図形です。 次の①から③にあてはまるものを 答えましょう。 (30 点) ① 頂 ちょう 点 てん bと対応する頂点 ② 辺bcと対応する辺 ③ 角cと対応する角線対称: 正三角形(対称の軸:3本)、正五角形(対称の軸:5本) 点対称: 平行四辺形 線対称かつ点対称: 正方形(対称の軸:4本)、正六角形(対称の軸:6本)、長方形(対称の軸:2本)、円(対称の軸:∞)線対称〇 対象の軸2本 点対称〇 <長方形> 線対称〇 対象の軸2本 点対称〇 <正方形> 線対称〇 対象の軸4本 点対称〇 〇p458の三角形も同様に調べよう <直角三角形> 線対称× 点対称× <二等辺三角形> 線対称〇 対象の軸1本 点対称〇 <正三角形> 線



Www Tsukuba Ed Jp Kuki2 Wp Content Uploads 04 Ba397da52e47dce9954f2b80fe45da14 Pdf



線対称と点対称について線対称でもあり 点対称でもある図形はどれで Yahoo 知恵袋
点対称な図形ではないが重心を中心とした1°の回転対称である。 内心 、 外心 、 垂心 、 重心 が全て一点に集まっている唯一の三角形である。 内心と外心が一致することから角の 二等分線 と対辺の 垂直二等分線 が一致し、この線で正三角形を2つに二等辺三角形 正三角形 直角三角形 線対称 対称の軸の本数;線対称 対称の軸の数 点対称 平行四辺形 ひし形 長方形 正方形 3 教科書Pを見て読んで、表の空欄をうめましょう。 線対称 対称の軸の数 点対称 正三角形 正方形 正五角形 正六角形 正七角形



線対称 点対称



Tossランド 対称な図形 多角形の性質
三角形 合同な図形 対称な図形 ・二等辺三角形,正三角形 ・合同の意味 ・線対称な形,点対称な形 の概念,性質,かき方 ・合同な三角形,四角形の の概念と性質 ・形としての角の概念,大 かき方 ・対称な図形の作図 小関係 ・対称性に着目した基本的6年 点対称な図形|算数イメージ動画集|大日本図書 文部科学省『教育用コンテンツ開発事業』 プロペラは1つの点を中心として 180° 回転させるともとの図形に重なるため,点対称な図形といえます。 点対称な図形では,対応する点を結ぶ線分は対称の2 点Oが対称の中心となるように、点対称な図形を書きなさい。 ①② 3下の a~ fの図形について次の問いに答えなさい。 ①線対称な図形を ②点対称な図形を ③線対称・点対称どちらで 答えなさい。 答えなさい。 もある図形を答えなさい。 A D C B E H G F



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun




6年算数対称な図形2 正多角形教え方
2.線対称でもあって,点対称でもある図形はどれかな? 問題 直角三角形,二等辺三角形,正三角形は,線対称な図形かな? 点対称な図形かな? 3.それぞれの三角形について調べよう。 直角三角形 二等辺三角形 正三角形・線対称、点対称の特徴 を見つけることができる ・平面上での2直線の位 置関係をとらえること ができる。 ・線対称や点対称の図 を見つけたり、かいた りすることができる。 ・図形の合同の意味がわ かる。 ・線対称、点対称の意味 や性質がわかる。エ すべての直角三角形は点対称でない。 オ 線対称になる直角三角形もあるが、すべての直角三角形が線対称であ るわけではない。 カ 点対称になる直角三角形もあるが、すべての直角三角形が点対称であ るわけではない。




Tossランド 対称な図形 多角形の性質



1
線対称か点対称か? 正三角形 線対称 対称の軸( )本 点対称 線対称でも点対称でもない 直角三角形 線対称 対称の軸( )本 点対称 線対称でも点対称でもない 二等辺三角形 線対称 対称の軸( )本(64)対称な図形 日 付 1 線対称 (1) 1つの直線を折り目にして 図形を折ったとき、ぴったり重なることを 何というでしょう。 (2) 次のアルファベットの中から、線対称な図形を 全て丸でかこもう。 (3) 次の正多角形の中から、線対称な図形を 全て丸で図形になる円は 線対称な 図形であり 点対称な 図形でもある 線対称 対称の軸の数 点対称 正方形 4 正六角形 6 正八角形 8 円 正五角形 正六角形 正七角形 正八角形 円 ・ 直角三角形 二等辺三角形 正三角形 線対称 対称の軸の数 点対称 頂点の数にも注目




線対称 点対称とは 具体例6選と応用問題3選で解説します 遊ぶ数学



6年算数対称な図形2 正多角形教え方
小6 算数「線対称・点対称」2 組 番氏名 (1)点o を対称の中心とした点対称な図形の残りの半分をかきましょう。 (2)次の正多角形について,線対称や点対称のときは ,そうでないときは×をかきま しょう。また,線対称のときは,対称の軸の数をかき例えば、フォーク、ジュースの缶や瓶は身近にある線対称な図形です xy平面上にy=f (x)の形で 奇関数 のグラフをかくと、原点を対称点とする点対称な図形になる ・身の回りにある対称な図形について,その美しさや安定性に着目しようとする。 ・既習の3 〇点対称について学ぼう。 教科書p14~17 ステップ2 4 〇点対称な図形をかこう。 教科書p18 ステップ3(2) 5 〇多角形と線対称・点対称について学ぼう。 教科書p19~ ステップ4 6 〇まとめの学習 うでだめシート 対称な図形①~③
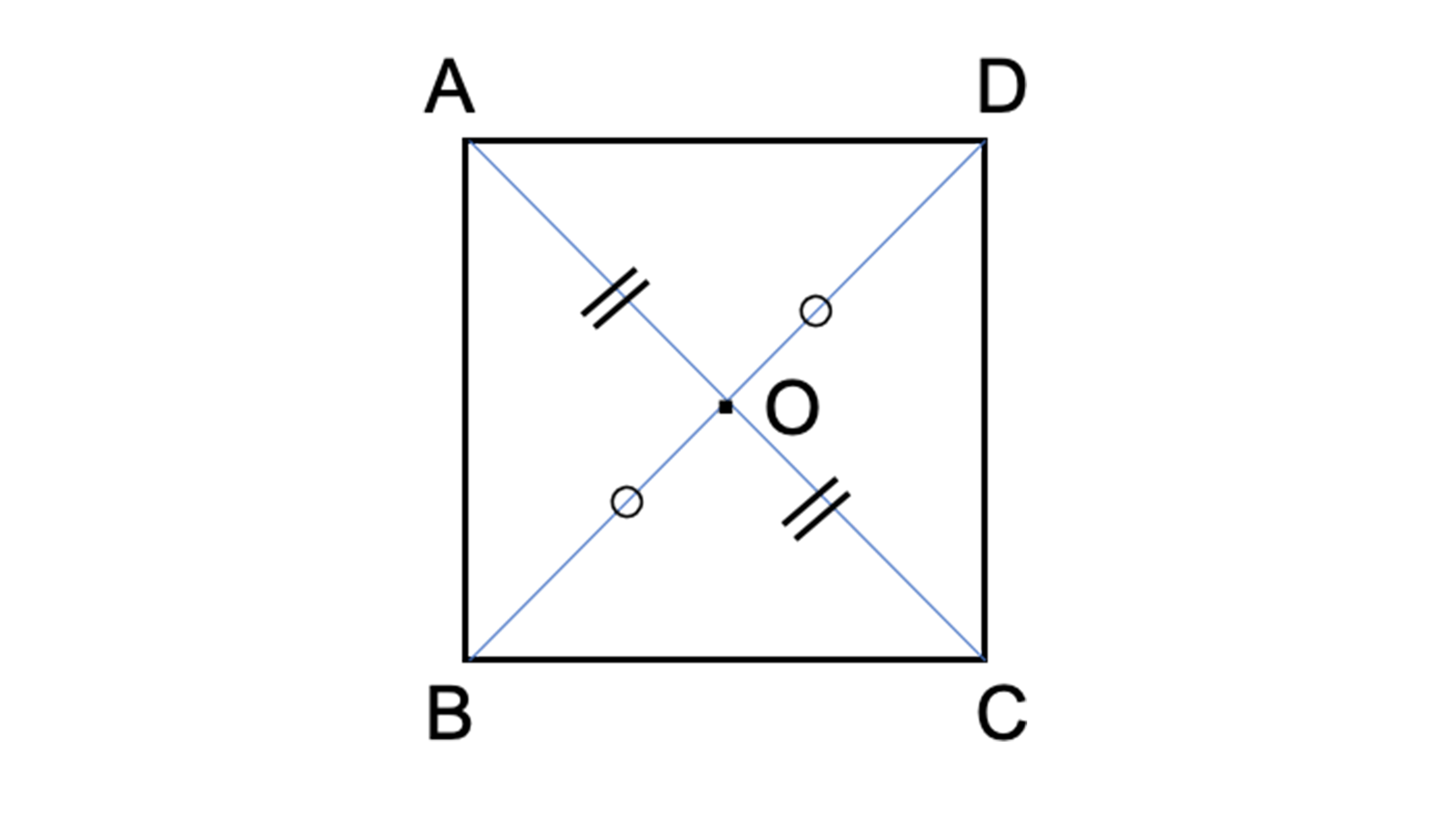



線対称との違いは 点対称 な図形を理解しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun
(1)点アを通り,直線イに平行な直線をか きなさい。 667 (2)点アを通り,直線イに垂直な直線をか きなさい。 3 (3)1 さい。 辺の長さが3cm の正三角形を,コンパスと定規を使ってかきな 100 2 線対称な図形をかきなさい。 75 3 点対称な図形を選びなさい。ア 正六角形 イ 正五角形 ウ 正四角形 エ 正三角形 o 点対称( ) 点対称( ☓ ) 点対称( ) 点対称( ☓ ) ふり返り ・折ってぴったり重なれば線対称、180°回して重なれば点対称。 ・正多角形は全て線対称線対称 対称の軸の数 点対称 ⑴ 平行四辺形 ⑵ ひし形 ⑶ 正三角形 ⑷ 正八角形 テーマ1 ・2 ⑴ ⑵ ア イ O テーマ1 ・2 A D C B E F テーマ3 ( ) ( ) テーマ3 テーマ3 _1_CoreSummer_Math_6nen_H_CC18indd 12 1627




教えてください Clear



多角形と対称 6年生 翁島 おきなしま 小学校ホームページ
① 線対称にはなっていないが,点対称になっている四角形 ② 線対称にも点対称にもなっており,対称の軸の数が8本の正多角形 4 ② 下の点対称な図形に対称の中心を かき入れましょう。 (かいた線は残しておきましょう。) 5 ② 点oが対称の中心になるように, 点対称な図形をかきましょう。線対称な図形ではない。(点線は、対称の 中心をみつけるためにひいている) (3) 正三角形は、線対称な図形であるが、 (4) 正方形は、線対称な図形でも点対称な図形でもある。 点対称な図形ではない。 (5) 正五角形は、線対称な図形であるが、対称⑴ 線対称 1 線対称 せんたいしょう とは 図のように、ある図形を1つの直線を折り目にして折ったとき、図 形がちょうど重なるなら、この図形は「直線について対称 たいしょう 」、「 線対称 せんたいしょう 」 といいます。



小6 対称な図形 三角形 日本語版 Youtube




三角形の対称性 スクールプレゼンター教材共有サイト スクプレ道場
ついて,線 せん 対 たい 称 しょう な図形か点対称な図形かを 調べ,記号で答えましょう。 〈各10点〉 線対称な図形 点対称な図形 下の図は,直線アイを対称の軸 じく とする 線対称な正五角形です。この図を見て 答えましょう。 〈各5点〉 ① 頂 ちょう直角三角形 二等辺三角形 正三角形 ①線対称な図形はどれですか。対称の軸をすべてかきましょう。 ②点対称な図形はありますか。 ( ) 18いろいろな正多角形について見なおしましょう。 正五角形 正六角形 正七角形 正八角形 ①線対称な図形はどれですか。新しい観点(線対称)気づくよう,段階的に図形を提示し,仲間集めの観点を考えさせていく。 (2) 線対称な図形を習得させる活動の工夫 「線対称な図形をさがしましょう。」 身の回りにある図形や点対称な図形なども入れておき,線対称の習得を図る。




対称の中心を使わずに点対称な図形をかく 算数を究める




3 Descubre Como Resolverlo En Qanda



正多角形と対称な図形



2




対称の英語 線対称 点対象 平行移動など 英語独学マスター



6年算数対称な図形2 正多角形教え方
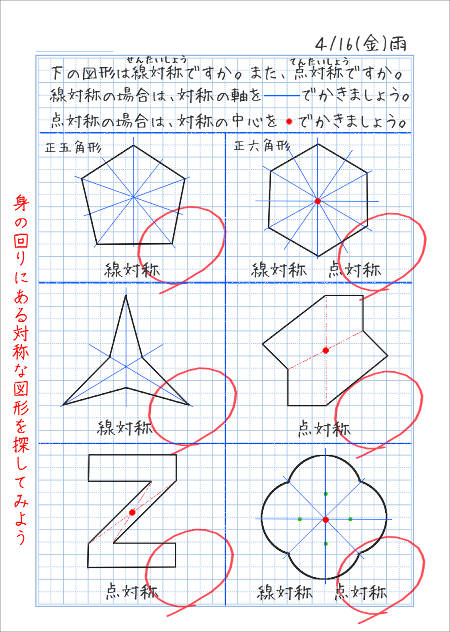



線対称と点対称の自主学習ノート 家庭学習レシピ




小6 対称な図形 四角形 日本語版 Youtube
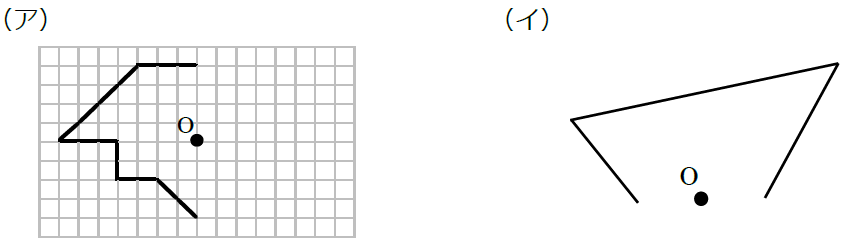



中1数学 点対称な図形とは まなビタミン




正三角形 Wikipedia




汚くてすみませんが もし良かったら図形に対称の軸をかいてください Clear



1



Www Kyo Kai Co Jp Img Material Shou 3056 Summer S6 Mihon Pdf



三角形を線対称図形に2分割 4 低次元日記




線対称で点対称な図形をかく 算数を究める
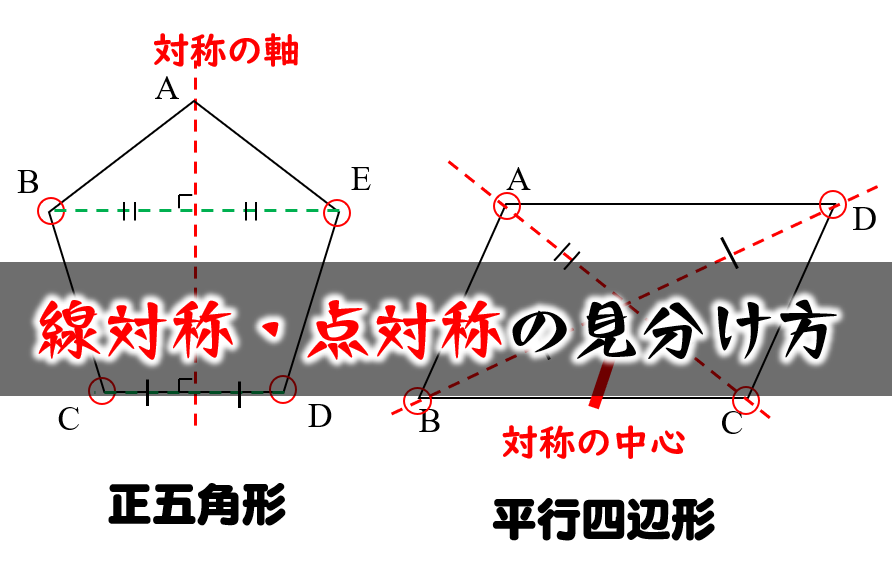



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



線対称 点対称



多角形と対称 6年生 翁島 おきなしま 小学校ホームページ



中学生の数学講座 線対称 点対称




対称な図形 多角形と対称 02 Youtube



Happylilac Net Pdf S6 Bun2 01 Pdf
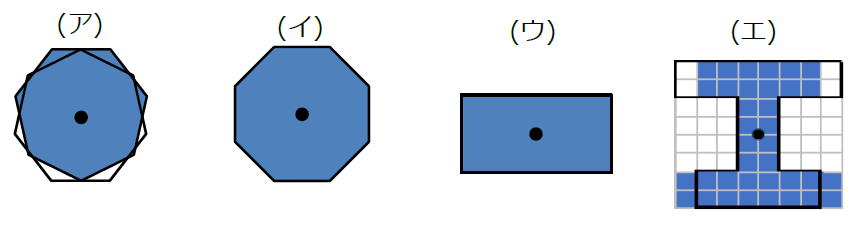



中1数学 点対称な図形とは まなビタミン




線対称 点対称とは 具体例6選と応用問題3選で解説します 遊ぶ数学



1



7 1 正多角形の線対称 点対称を求めるには さんすうがく パート 2
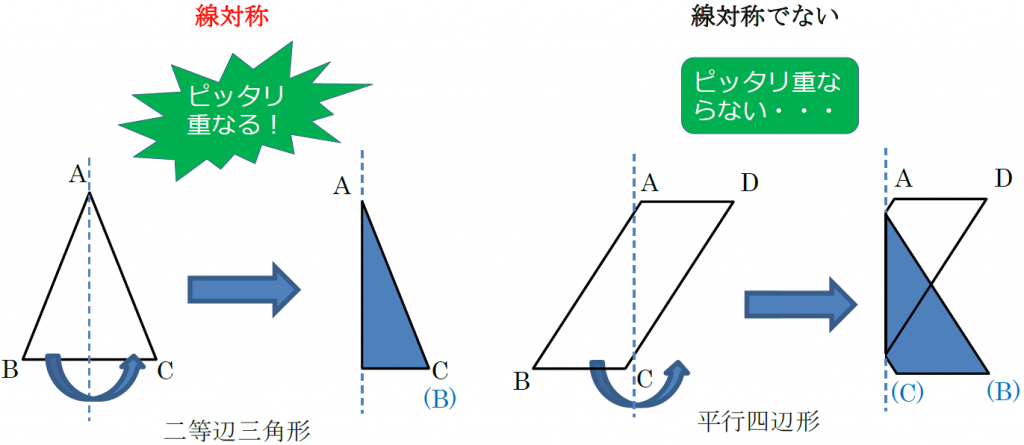



中1数学 点対称な図形とは まなビタミン



無料 中1数学 標準問題 解答プリント 136 平面図形3 平面図形の作図



中1数学 点対称な図形とは まなビタミン



Http Www Edu Ctr Pref Nagano Lg Jp Kjouhou Manabi Hiroba 05 Review Mondai Mondai S Re Sho6 01 03 Pdf



2



1



線対称 点対称




線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



6年算数対称な図形2 正多角形教え方



4 5 直角三角形に垂線を引いた時の辺の長さを求めるには さんすうがく パート 2



中学数学 線対称な図形 中学数学の無料オンライン学習サイトchu Su



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



中学数学 点対称な図形 中学数学の無料オンライン学習サイトchu Su
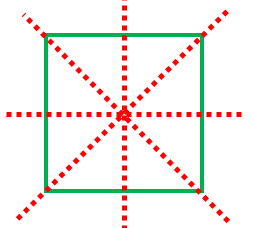



対称の軸 線対称の意味と 正多角形などでの本数 具体例で学ぶ数学



6年算数対称な図形2 正多角形教え方




高校数学 三角形の形状 正三角形 二等辺三角形 直角三角形 受験の月



Http Www E Tokoji Hino Tky Ed Jp Action Common Download Main Upload Id 2803
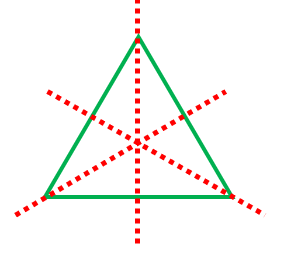



対称の軸 線対称の意味と 正多角形などでの本数 具体例で学ぶ数学
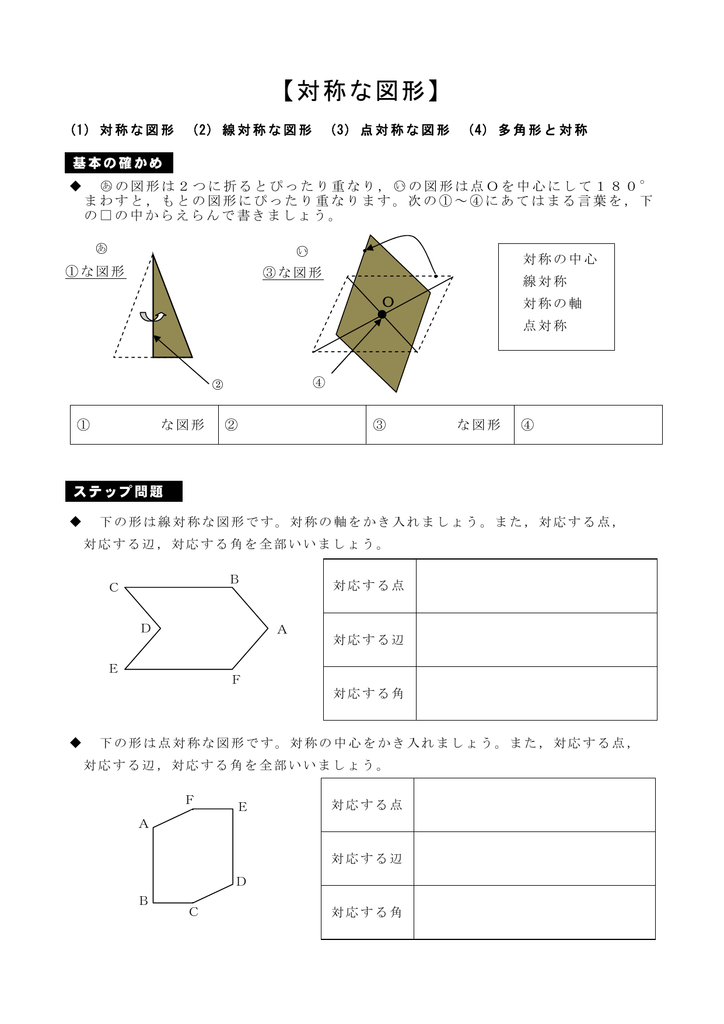



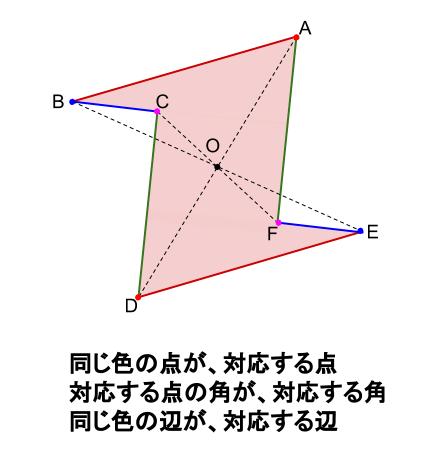
対称な図形



6年算数対称な図形2 正多角形教え方




線対称と点対称 小6 再度確認と定着 算数の教え方教えますmother S Math Happy Study Support



2



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun
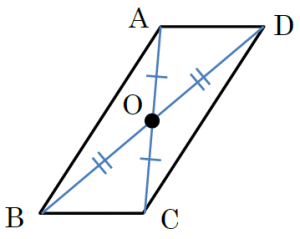



中1数学 点対称な図形とは まなビタミン



Www Pref Chiba Lg Jp Kyouiku Shidou Gakuryoku Cc100 Sannsuu Documents S6 013 Pdf



線対称図形と点対称図形の見分け方 算数解法の極意




線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



Http Www Toyohashi Ed Jp E Kodomo Print45 Sansuu E6taisyou Kai Pdf



2




悩みのタネ 解決編 線対称と点対称 声に出さないけど思っていること



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun



長方形 平行四辺形 正方形 二等辺三角形 正三角形 線対称な図形を Yahoo 知恵袋
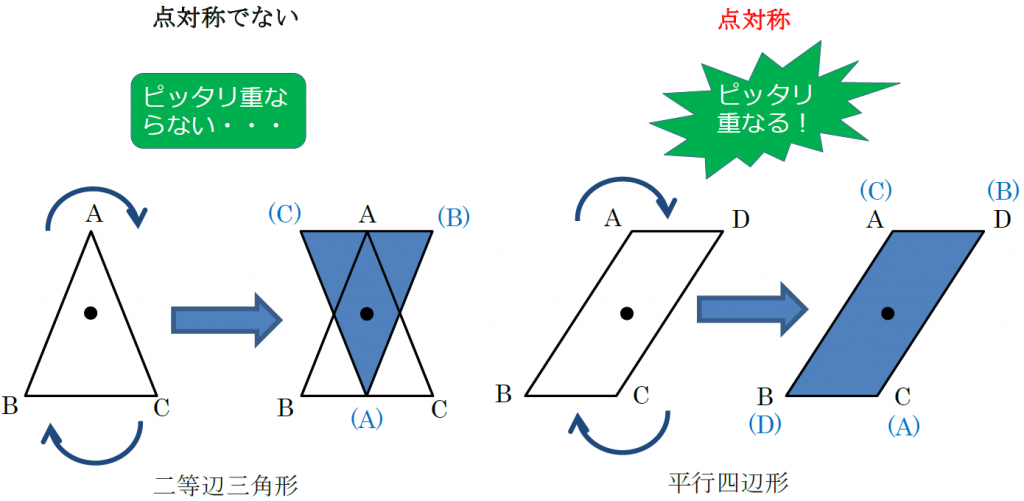



中1数学 点対称な図形とは まなビタミン
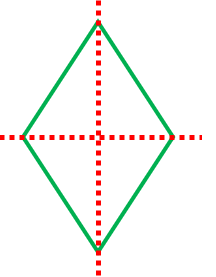



対称の軸 線対称の意味と 正多角形などでの本数 具体例で学ぶ数学



算数の点対称のことについてです 長方形正方形ひし形正六角形正八角形二等 Yahoo 知恵袋




スマホok 6年 対称な図形 多角形と対称 Youtube




対称の授業 算数



2



Http Www2 Kobe C Ed Jp Krb Es Action Common Download Main Upload Id




線対称 点対称




スタディギア 折って回して考えよう Facebook




3c0 Com Support Service Descubre Como Resolverlo En Qanda



Ichikawa School Ed Jp Ichikawa Sho Cabinets Cabinet Files Download 31 8b03bb31bfa6045d54e81bdb0f8d1a Frame Id 52




線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun




線対称 点対称 算数用語集




Descubre Como Resolverlo En Qanda
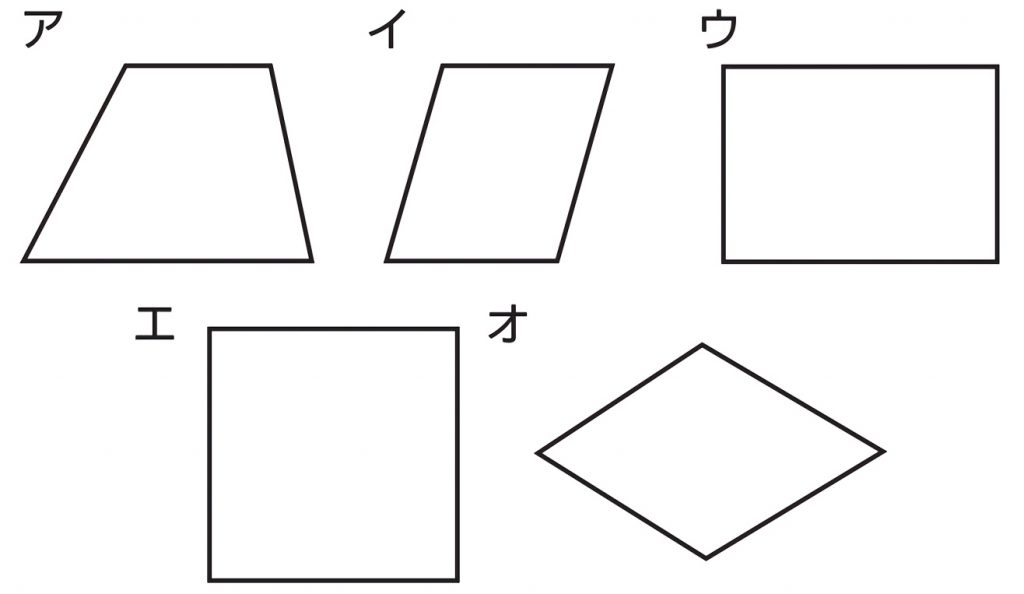



小6算数 多角形と対称 指導アイデア みんなの教育技術



Http Www Kita9 Ed Jp Yugawa E Gakusyuu621 Pdf
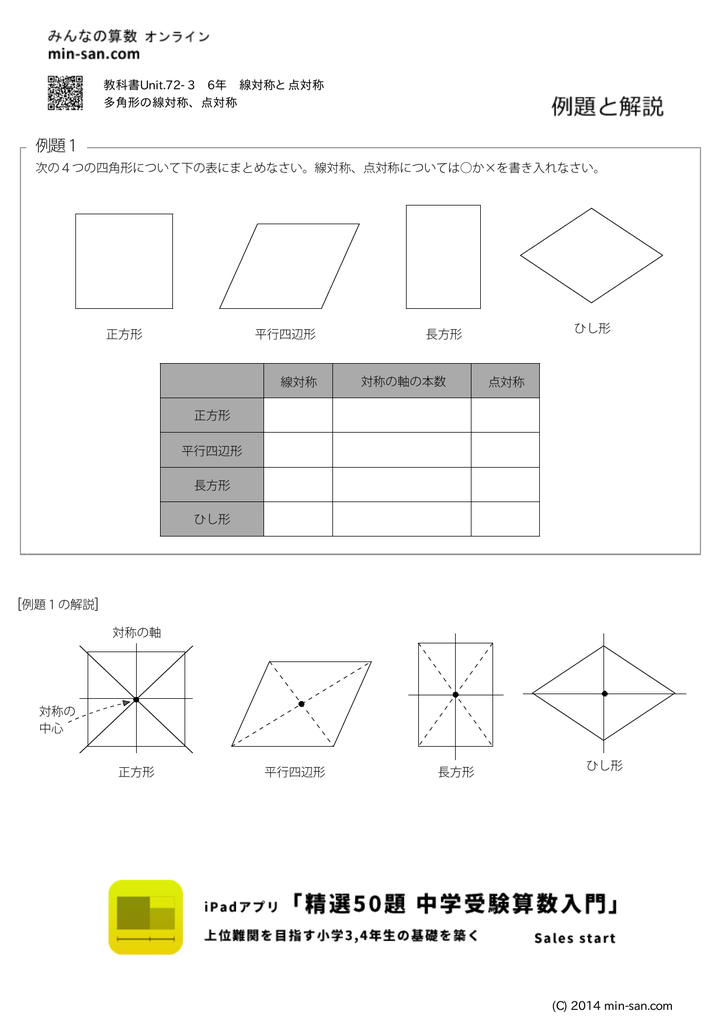



例題1




小学総まとめ 対称図形 きっずゼミ子育て応援ブログ
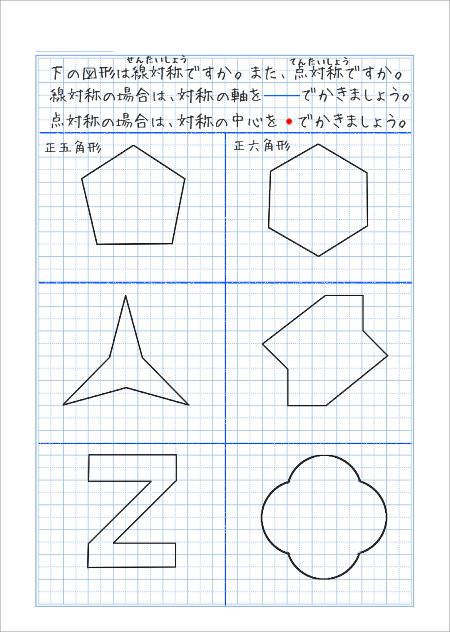



線対称と点対称の自主学習ノート 家庭学習レシピ



正七角形は線対称ですか 点対称ですか 奇数の正多角形は線対称 偶数の正 Yahoo 知恵袋



線対象 点対称算数問題が解けません よくわからないので教えてください Yahoo 知恵袋



Descubre Como Resolverlo En Qanda
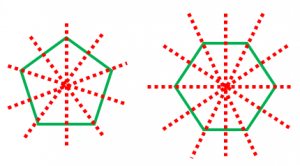



対称の軸 線対称の意味と 正多角形などでの本数 具体例で学ぶ数学
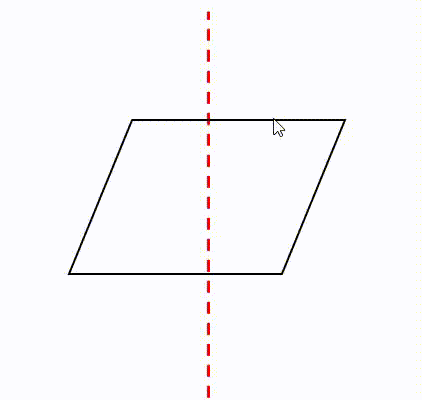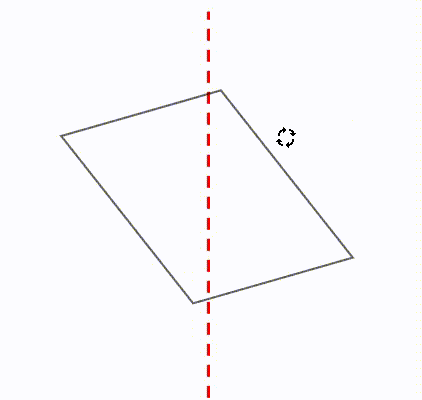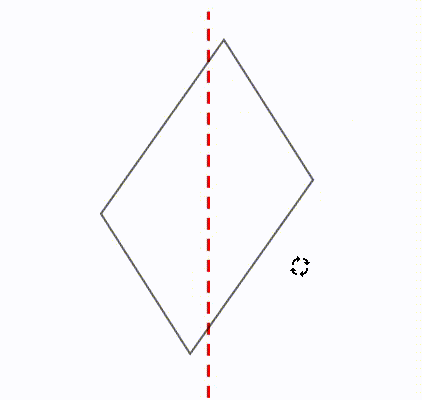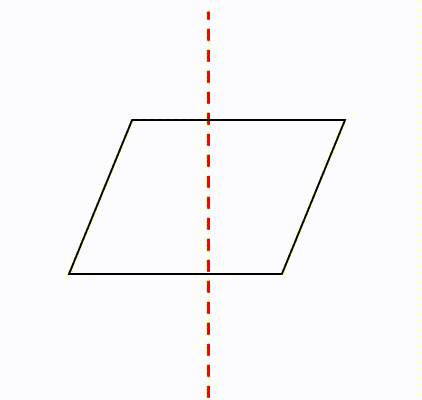



線対称 点対称の定義と違い 簡単な見分け方を解説 数学fun




図形の見直し 授業がんばりmath




小6 算数 小6 14 多角形と対称 Youtube
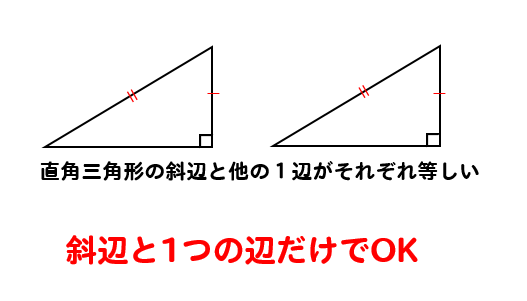



直角三角形の合同条件 証明問題の書き方とは イチから徹底解説 数スタ



多角形と対称 6年生 翁島 おきなしま 小学校ホームページ
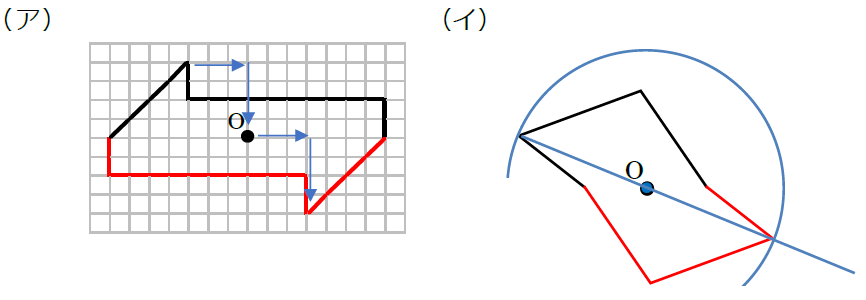



中1数学 点対称な図形とは まなビタミン


